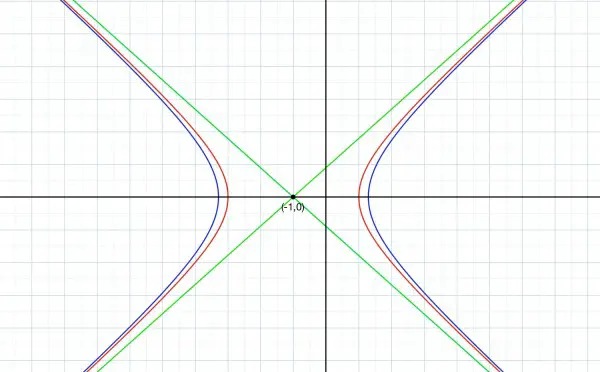
k(x,y)=4x²+8x-5y²+3=4(x²+2x+1-1)-5y²+3=
4(x+1)²-5y²+3-4=4(x+1)²-5y²-1.
I presume that k(x,y)=c so 4(x+1)²-5y²-1=c for the values given.
When c=-1 we get the crossed lines part of the graph shown in green. These are asymptotes for the other two hyperbolas. The equations of the hyperbolas (or straight lines) can be found by substituting c=-1, 15 and 20. The graphs represent cross-sections of the 3-dimensional shape defined by k at various points along the z-axis where z=k(x,y). This axis can be imagined as pointing directly at the viewer, so you are looking along the axis through the 3D shape as if it were transparent. The centre of the hyperbolas and the intersection of the lines are all on the same axis where x=-1 and y=0, because in 3D a point becomes an axis. The red hyperbola corresponds to c=15 and the blue to c=20. The red hyperbola passes through the points (1,0), (-3,0), (2,2), (-4,2), (2,-2), and (-4,-2).