z1 and z2 are two non zero complex numbers.prove that 2|z1+z2|>or= (|z1|+|z2|)|(z1/|z1|)+(z2/|z2|)|

Question

question is from the exercise of higher algebra by s k mapa

Answer 1

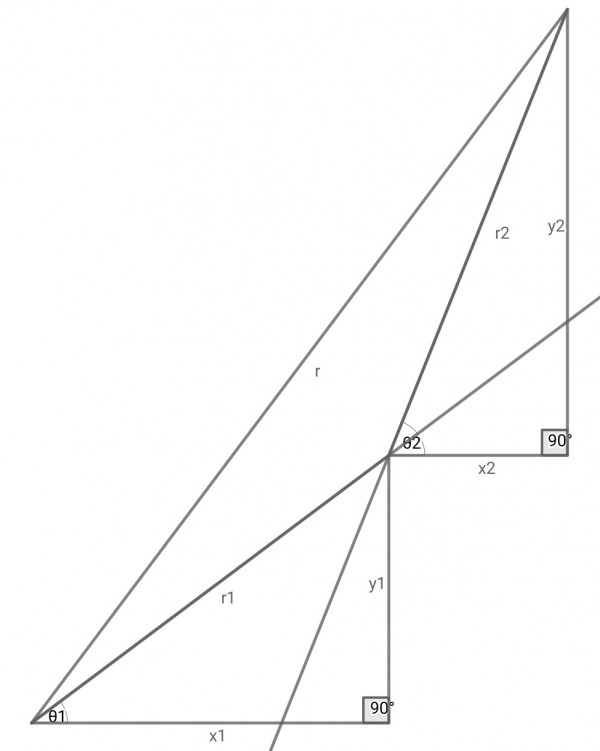
The complex numbers are represented above geometrically.

z=z1+z2=x+iy, z1=x1+iy1, z2=x2+iy2,

r=|z1+z2|, r1=|z1|, r2=|z2|, 

sinθ1=y1/|z1|=y1/r1, cosθ1=x1/|z1|=x1/r1,

sinθ2=y2/|z2|=y2/r2, cosθ2=x2/|z2|=x2/r2,

z1/|z1|=(x1+iy1)/r1=cosθ1+isinθ1,

z2/|z2|=(x2+iy2)/r2=cosθ2+isinθ2.

The question becomes to prove:

2r≥(r1+r2)|cosθ1+isinθ1+cosθ2+isinθ2|,

2r≥(r1+r2)|cosθ1+cosθ2+i(sinθ1+sinθ2|)|.

We can now use the trig identities:

cosA+cosB≡2cos[½(A+B)]cos[½(A-B)],

sinA+sinB≡2sin[½(A+B)]cos[½(A-B)].

2r≥2(r1+r2)|cos[½(θ1+θ2)]cos[½(θ1-θ2)]+i2sin[½(θ1+θ2)]cos[½(θ1-θ2)]|,

r≥(r1+r2)|cos[½(θ1+θ2)]cos[½(θ1-θ2)]+isin[½(θ1+θ2)]cos[½(θ1-θ2)]|,

r≥(r1+r2)√(cos²[½(θ1+θ2)]cos²[½(θ1-θ2)]+sin²[½(θ1+θ2)]cos²[½(θ1-θ2)]),

r≥(r1+r2)cos[½(θ1-θ2)].

Since cosA≡2cos²(A/2)-1, cos²(A/2)=(1+cosA)/2,

r≥(r1+r2)√[(1+cos(θ1-θ2))/2].

We know that cosine ranges between -1 and 1, so (1+cos(θ1-θ2))/2 ranges between 0 and 1, therefore the expression on the right of the inequality has a range 0 to r1+r2, making the inequality true. When θ1 and θ2 differ by 180º or π radians, r=0, and when θ1=θ2, r=r1+r2, when r1 and r2 lie along r, so we no longer have a triangle.