At 1pm the distance x between them is 150m (time t=0 hr). The question doesn’t state another distance and bearing at t=0, so we assume the ships are initially on a north-south line.
An hour later (t=1 hr) at 2pm, A has moved 30 further north and B 20m further south, so they are 50m further apart, and x=150+50=200m.
At 3pm, t=2, they are another 50m apart and x=250m.
So each hour they are separating at a rate of 50mph.
The equation is x=150+50t. But the rate is constant at 50mph. At 3pm they are still moving apart at 50mph.
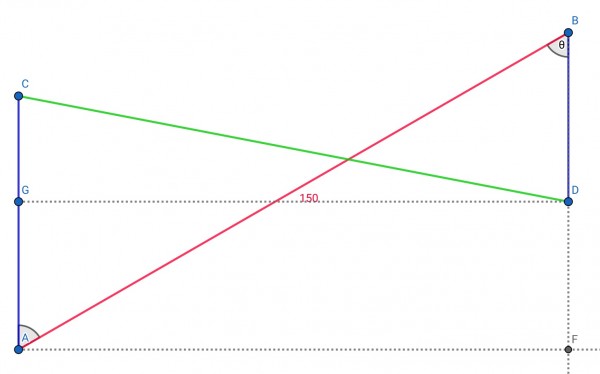
In the more general case, the ships are 150m apart at t=0, but ship B is on a bearing of θ degrees (from north). In the picture the red line AB (length 150 miles) represents the ships in their initial positions. After time t, the blue lines show the distance the ships have travelled: A moves 30t miles north to point C while B moves 20t miles south to point D. The bearing is angle CAB=ABF=θ. The green line CD is their distance apart after t hours.
So BF=150cosθ, DG=AF=150sinθ, AC=30t, BD=20t, AG=DF=BF-BD=150cosθ-20t, CG=AC-AG=30t-150cosθ+20t=50t-150cosθ.
By Pythagoras’ Theorem, AB²=150²=AF²+BF² and CD²=CG²+DG².
Let x=CD, then x²=(50t-150cosθ)²+(150sinθ)².
x²=(50t)²-2(50t)(150cosθ)+(150cosθ)²+(150sinθ)²,
x²=2500t²-15000tcosθ+22500.
x=√(2500t²-15000tcosθ+22500).
dx/dt is rate at which distance is increasing (or decreasing). θ is a constant initial condition.
dx/dt=½(5000t-15000cosθ)/√(2500t²-15000tcosθ+22500).
dx/dt=(2500t-7500cosθ)/√(2500t²-15000tcosθ+22500).
We can divide through by 50 to simplify this:
dx/dt=50(t-3cosθ)/√(t²-6tcosθ+9).
If we put t=2 hr (3pm), we get:
dx/dt=50(2-3cosθ)/√(13-12cosθ).
EXAMPLES
θ=180º, dx/dt=250/√25=50 mph. This means that the ships were heading in opposite directions on the north-south line (as the question implies).
θ=0º, dx/dt=-50 mph, because both ships are moving north, but B was 150 miles ahead of A, so the distance and the rate are decreasing as A catches up with B.
θ=60º, dx/dt=25/√7=25√7/7=9.45 mph approx.
θ=90º, dx/dt=100/√13=27.74 mph approx. (Ship B started 150 miles east of A.)