((x^2-1)/sqrt(2x-1) )
\cdot%20(2x-1)^{-0.5}%20\;%20dx "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
Integrating by parts - let u= x^2-1 so u' = 2x, let v' = (2x-1)^-0.5 so v= 2(2x-1)^0.5
(int by parts formula)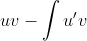 
\cdot%202\;%20\sqrt{2x-1}%20-%20\int%202x%20\cdot%20\sqrt{2x-1}%20\;%20dx "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
Integrating by parts again - u=2x, u'=2 v'= 2(2x-1)^0.5, so v=2/3 (2x-1)^1.5\cdot%202\;%20\sqrt{2x-1}%20-%20(2x\cdot%20\frac{2}{3}(2x-1)^{3/2}%20-%20\frac{4}{3}%20\int(2x-1)^{3/2}) "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
\cdot%202\;%20\sqrt{2x-1}%20-%20(2x\cdot%20\frac{2}{3}(2x-1)^{3/2}%20-%20\frac{4}{3}%20\cdot%20\frac%20{1}{5}(2x-1)^{5/2})%20+%20k "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
Feel free to tidy this one up, but the hard part is done :P Also, if i have done any part wrong, please message me as i kept confusing myself with the latex code which is designed to make it easier!