With three unknown prices and only two equations it’s not possible to find the cost of each item. More information would be needed. In this case, because the price of an item can be a decimal fraction of a dinar extending to three places of decimals, many solutions would be possible. The best that can be done is to relate the prices of two of the items in terms of the third item.
Another approach is to assume that prices are realistic, that is, the price of each item falls in a given range. This reduces the number of possibilities, but doesn’t necessarily lead to a unique solution.
In conclusion, there is insufficient information to determine uniquely the price of each individual chocolate.
ADDENDUM
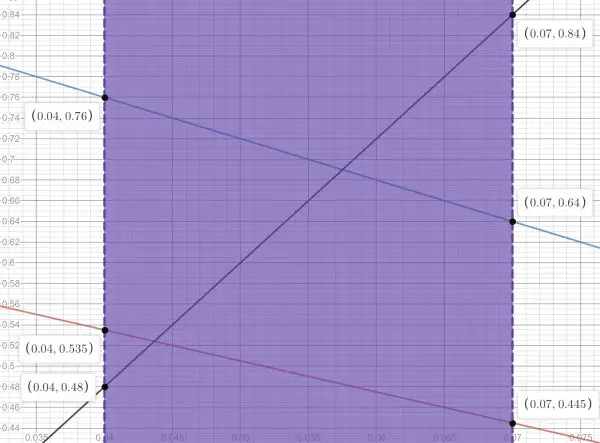
The picture shows a shaded area representing the price of each individual item, if it’s assumed that the price of KitKat is in the range 0.48-0.84BD.
The red line represents Snicker prices and the blue line Galaxy prices. The black line converts the x value into KitKat prices.
This picture shows that, when KitKat costs the minimum of 0.48BD, Snicker costs 0.535BD and Galaxy 0.76BD; and it shows that, when KitKat costs the maximum of 0.84BD, Snicker costs 0.445BD and Galaxy 0.64BD. The graph is useful for finding the prices for Snicker and Galaxy bars for 7 feasible prices of KitKat (0.48, 0.54, 0.60, 0.66, 0.72, 0.78, 0.84). Just trace the intersection of any of the vertical lines (0.04, 0.045, etc.) with the black (KitKat), red (Snicker) and blue (Galaxy) lines to find the cost of each.