A dozen balls (12) is 3 sets of 4 balls, so one set of 4 balls costs $60/3=$20. But there will be 3 extra balls (one for each set), that is, 12+3=15 balls for the cost of 12.
$144 will buy 144/20=7 sets (28 balls) costing $140. 7 extra free balls will be added, making 28+7=35 balls altogether. 1 set costs $20 so each ball costs $5. But there is only $4 left, not enough to buy another ball. Therefore $144 will buy 28 balls plus 7 free balls, 35 balls in all, and there will be $4 in change.
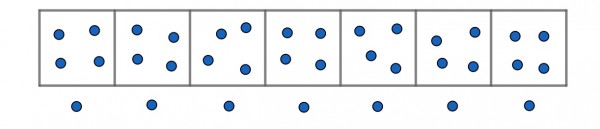
In the picture below each box contains 4 balls. Three boxes contain a dozen balls and cost $60. There are 7 boxes, containing 28 balls. 6 boxes cost $120 and the 7th box costs $20 (one third of $60) so the total cost (what is actually bought or paid for) is $140. The balls outside the boxes are free as a result of the offer, so $140 pays for 28 balls and 7 balls come free, making 35 in all. A box of 4 balls costs $20, so there isn’t enough change ($4) out of $144 to pay for another ball.
If you use the wrong logic and assume that 5 balls costs $20, each ball would appear to cost $4, not $5, and there would be enough change to buy another ball, making 36 balls altogether, but this is false logic! This question was designed to make you think more logically. It’s a sort of trick question.