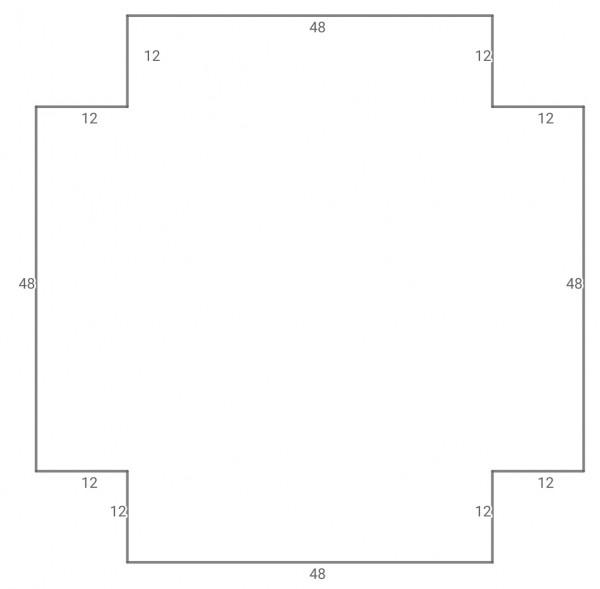
If the side of the squares cut out from the corners is x inches, then the dimensions of the box are length=width=72-2x and height=x, and volume V(x)=(72-2x)²x=4(36-x)²x=4x(1296-72x+x²)=5184x-288x²+4x³.
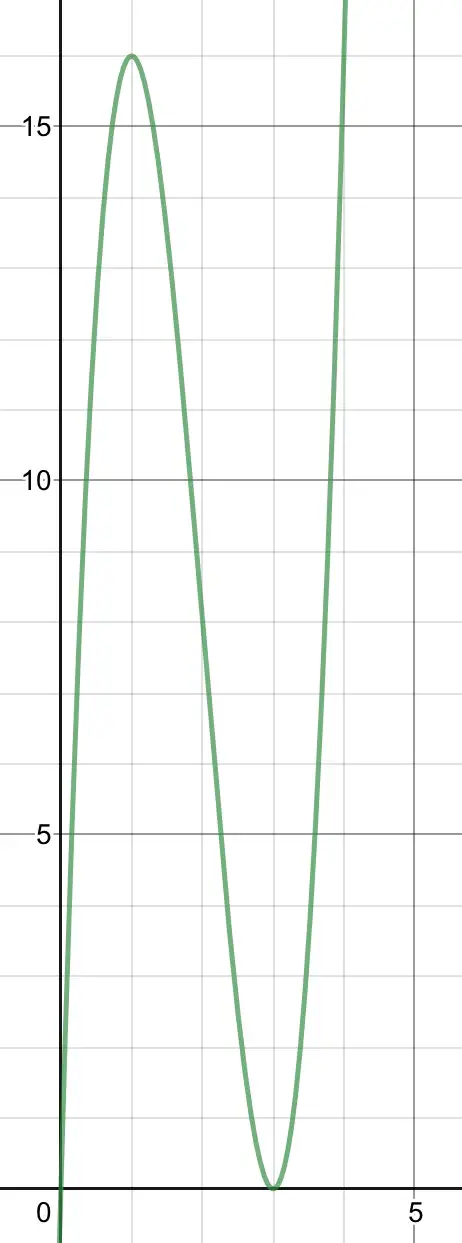
The graph shows V(x) where x is in feet. The maximum and minimum can be clearly seen.
dV/dx=5184-576x+12x²=0 at extrema. This quadratic reduces to:
432-48x+x²=0=(x-36)(x-12), making x=36 or 12. We can reject x=36 because V(36)=0 (minimum).
V(12)=27648 cubic inches=16 cubic feet.