The slope of OC is -2/4=-½, so the slope of DE must be -(1/½)=2 and the equation of DE is y-3=2(x+3/2), that is, y=2x+6. We can only determine the size of the circle by assuming that C is on the circumference.
OC²=(-4)²+2²=16+4=20 and OC is a radius, and OC=OD=OE. We can work out the equation for OC, y=-x/2, because we know its slope and it passes through the origin. The equation of the circle is x²+y²=20 because OC is a radius. The chord line intersects the circle at D and E. If we substitute y=2x+6 into the equation of the circle, we have x²+(2x+6)²=20.
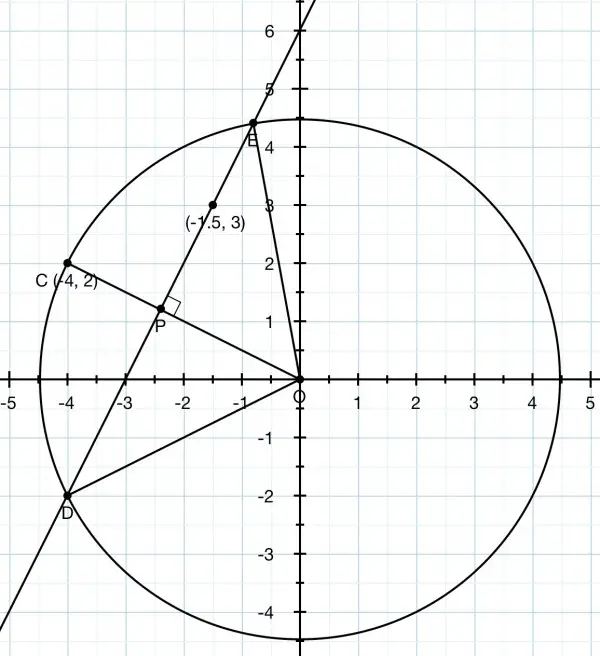
x²+4x²+24x+36=20, 5x²+24x+16=0=(5x+4)(x+4). Therefore x=-4/5 and -4 giving us the x-coords for D and E.
The corresponding y coords are 2(-4/5)+6=22/5, and 2(-4)+6=-2. So the coords of D and E are (-4/5,22/5) and (-4,-2).
(We could have worked out the answer geometrically by calculating the coords of P and using Pythagoras’ Theorem for working out the length of EP and DP (which are the same), and deduce the coords that way, but the graphical solution is the quicker method.)