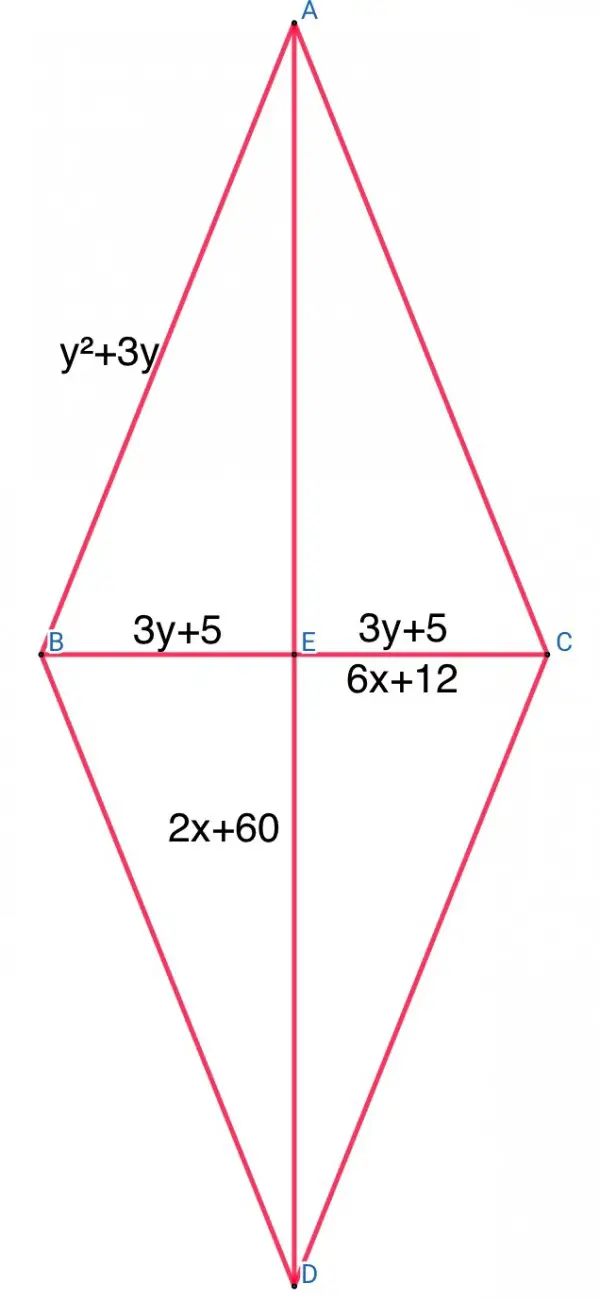
Since no picture has been provided for this question, I have to assume that AE is the median from A to BC, so E is the midpoint of BC. Also, DE is the median from D to BC. D and A could be on the same or opposite side of BC. Therefore, BE=CE and BC=2BE=2CE, CE=BE=6(x+2)=3y+5, from which 3y=6x+7. There are two principal triangles ABC and DBC with a common base BC.
FIRST SOLUTION
The given information is not sufficient of itself to find specific values for x and y, so a rhombus ACDB has been used to supply the geometry which leads to a solution. ABC and DBC are congruent isosceles triangles.
CD²=(6x+12)²+(2x+60)²=
40x²+384x+3744=
AB²=(y²+3y)²=y²(y+3)²=y⁴+6y³+9y².
We have 3y=6x+7, so we can substitute for y or x and solve.
2x=y-7/3, 2x+60=y+173/3.
Let’s substitute 3y+5 for 6x+12:
9y²+30y+25+y²+346y/3+29929/9=y⁴+6y³+9y².
y⁴+6y³-y²-436y/3-29929/9=0.
An approximate solution is y=7, so we can use Newton’s Method to get a more accurate answer.
y=y-(y⁴+6y³-y²-436y/3-29929/9)/(4y³+18y²-2y-436/3).
y=6.9697 approx. So x=2.3172 approx. AB=69.4519, BC=51.8062, CE=25.9031, DE=64.6344.
More to follow...