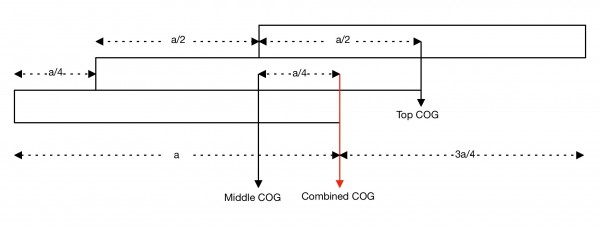
Assume that the weight of each brick acts at its centre, a distance a/2 from either end.
We start with the top and middle bricks. The centre of gravity (COG) of the top brick cannot be positioned beyond the edge of the middle brick, otherwise it would fall off. So the equilibrium position for the top brick is a displacement of a/2 over the middle brick.
The COG of the two bricks is midway between the COGs of each brick. This makes the combined COG halfway between the COG of the middle brick and its end, that is, 3a/4, three-quarters its length.
The combined COG must be positioned no further than the end of the bottom brick. This means that the displacement of the middle brick over the bottom brick can only be a/4. In this position, the combined COG sits at the end of the bottom brick, and the middle brick overhangs the bottom brick by a/4.
So looking at the entire assembly, the top brick's displacement is a/2 and the total displacement, d, of the top brick is a/2+a/4=3a/4.