Let B be the number of hours baby-sitting and M the number of hours mowing the lawn.
M+B≤12 (no more than 12 hours a week working).
8M+12B≥100 (combined earnings must be at least $100).
This reduces to 2M+3B≥25.
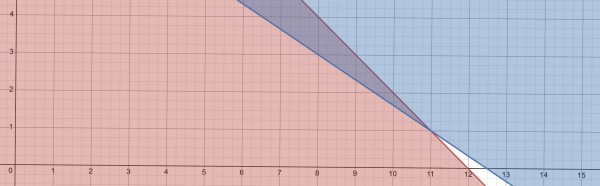
M is the horizontal axis and B the vertical axis.
The red line and shaded area represents M+B≤12 while the blue line and shaded area represents 2M+3B≥25.
The darker shading is where both inequalities are satisfied. All points within this dark region fulfil both inequalities.
Where the lines cross, M=11 and B=1, that is, 11 hours mowing and 1 hour baby-sitting. Earnings=88+12=$100.
Another solution: 8 hours mowing, 3 hours baby-sitting. Total time 11 hours. Earnings=64+36=$100.
Another solution: 8 hours mowing, 4 hours baby-sitting. Total time 12 hours. Earnings=64+48=$112.
Another solution: 4 hours mowing, 8 hours baby-sitting. Total time 12 hours. Earnings=32+96=$128.
Maximum earnings when M=0, 12 hours baby-sitting, earnings=$144.
Minimum time=8⅓ hours, earnings from baby-sitting and no mowing=$100.