I have an assignment due at 11:59pm I can send you the pdf through email.

Question

Directions:  
 
This project contains multiple parts. Each part of the project contains several questions. Answer each question to the best of your ability and record your answer in a separate document (do not enter the answers on the project itself) and upload your work, in the proper format, to the appropriate “Assignment” within Falcon Online by the posted due date.  
 
You may work individually on this project or you may work in a group of up to 3 students. If you choose to work within a group, each member of the group must upload the group’s submission.
 
 
Submission Format Instructions:
 
1. Your submission must be a single, typed document saved as a Word document (.doc or .docx), Rich Text Format (.rtf), or a Portable Document Format (.pdf).
 
2. Your name must be at the top of your submission. If you worked in a group the names of every group member must be included at the top of your submission.  Each person in the group must submit a completed application to the Assignments link in Falcon Online (be sure to click on “Submit” after using the “Add a File” link.
 
3. Do not type the questions from the project into your submission. You should submit only your answers to the questions along with any calculations used to obtain the answer.  You can use a calculator to do the work, but you must show the information used to answer the question and/or the values entered into the calculator.
 
4. Follow the numbering system used in the project when typing your answers.
 
 
 
Failure to follow the directions or submission format instructions will result in loss of points.
 
 
If you do not submit your work by the due date it will not be accepted for grading.
 
 
Speak with your instructor as they may have additional requirements for your submission.
 
 
 
 
 
 
 
 2
 
Part 1:  Linear Programming Problem 1
 
A confectioner sells two types of nut mixtures. The standard-mixture package contains 100 g of cashews and 200 g of peanuts and sells for $1.95. The deluxe-mixture package contains 150 g of cashews and 50 g of peanuts and sells for $2.25.
 
The confectioner has 15 kg of cashews and 20 kg of peanuts available. On the basis of past sales, the confectioner needs to have at least as many standard as deluxe packages available. How many bags of each mixture should she package to maximize her revenue?
 
For this problem we will let x represent the number of standard-mixture packages and let y represent the number of deluxe-mixture packages. The values of x and y that will maximize her revenue depend on the amount of cashews and peanuts available for use.
 
 x = number of standard-mixture packages  y = number of deluxe-mixture packages
 
This information is used to create constraint equations because they constrain the possible values of the variables.
 
 
Constraint Equation 1:
 
There are 15 kg, or 15,000 g, of cashews available.   Since the standard-mixture uses 100 g and the deluxe-mixture uses 150 g we must make sure that
 
 100x + 150y ≤ 15,000
 
Dividing the inequality by 50 gives:  2x + 3y ≤ 300
 
 
Constraint Equation 2:
 
There are 20 kg, or 20,000 g of peanuts available.  Since the standard-mixture uses 200 g and the deluxe-mixture uses 50 g we must make sure that
 
 200x + 50y ≤ 20,000
 
Dividing the inequality by 50 gives:  4x + y ≤ 400
 
 
Constraint Equation 3:
 
The problem also states that she needs to have at least as many standard as deluxe packages available so we need
 
  x ≥ y , which can be expressed as:  y ≤ x
 
 3
 
Constraint Equations 4 and 5:
 
 Lastly, since she cannot produce a negative number of packages it must be that
 
  x ≥ 0 and y ≥ 0
 
 
The goal of this problem is to find the values of x and y that maximize her revenue. Since the standard-mixture sells for $1.95 and the deluxe-mixture sells for $2.25, her revenue will be given by the equation
 
 R = 1.95x + 2.25y
 
If we plot the constraint equations on the same set of axes, the ordered-pair, (x,y), that maximizes her revenue will be a vertex (corner; intersection of 2 lines) of the “feasible region.” The feasible region is the graph of the constraints and can be seen here.
 
 
 
 
 
 
 
 
 
 
 
 4
 
Part 1 Exercises:  
 
1. Find the coordinates of the vertices of the feasible region.  Clearly show how the vertex is determined and which lines form the vertex.  a. Find the coordinates of vertex 1.  b. Find the coordinates of vertex 2.  c. Find the coordinates of vertex 3.  d. Find the coordinates of vertex 4.
 
2. Find the value of R for each vertex.  a. Calculate R for vertex 1.  b. Calculate R for vertex 2.  c. Calculate R for vertex 3.  d. Calculate R for vertex 4.
 
3. How many standard-mixture packages and how many deluxe-mixture packages should she sell to maximize her revenue?
 
 
 
 
Part 2:  Linear Programming Problem 2
 
Consider the feasible region in the xy-plane defined by the following linear inequalities.
 
 x ≥ 0  y ≥ 0  x ≤ 10  x + y ≥ 5  x + 2y ≤ 18
 
 
Part 2 Exercises:  
 
1. Find the coordinates of the vertices of the feasible region.  Clearly show how each vertex is determined and which lines form the vertex.
 
2.  What is the maximum and the minimum value of the function Q = 60x+78y on the feasible region?

Answer 1

First a picture to make things clearer:

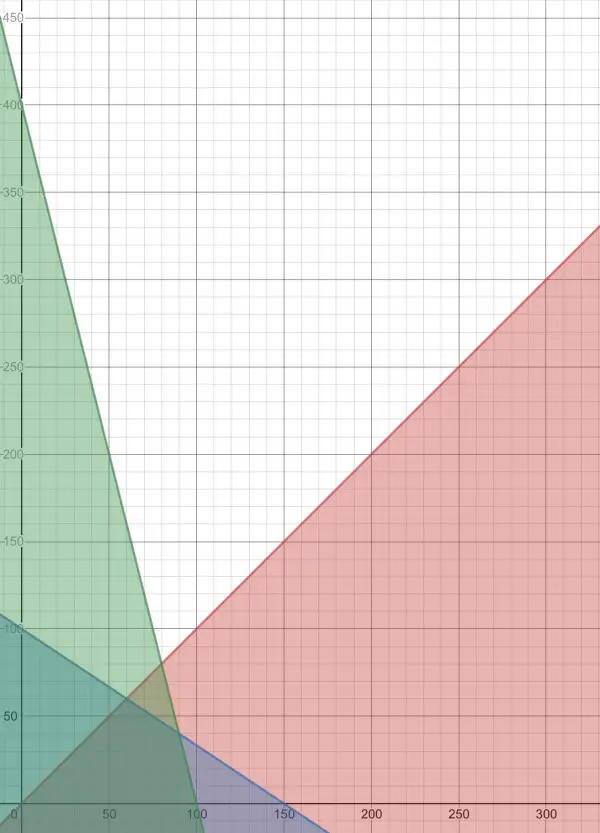
CONSTRAINT 1 is blue, CONSTRAINT 2 is green, CONSTRAINT 3 is red. CONSTRAINTS 4 and 5 mean that we only consider the first quadrant of the graph. The blue, green and red lines are the constraint equations shown graphically, while the shaded regions represent the inequalities. Where all three shaded regions overlap is the feasible region, and we just need the vertices of this region, which form a quadrilateral with one vertex at the origin.

We need the coordinates of the vertices. A vertex is formed where two lines intersect.

The equations we use can be written:

y=100-⅔x (blue), y=400-4x (green), y=x (red).

Red and green intersect when 400-4x=y=x; solve 400-4x=x, 5x=400, x=80=y. Intersection is (80,80), but this is outside the feasible region. Red and blue intersect when 100-⅔x=y=x; solve 100-⅔x=x, 5x/3=100, x=60=y. This point (60,60) is a vertex of the feasible region.

Green and blue intersect at another vertex of the feasible region:

100-⅔x=y=400-4x; solve 100-⅔x=400-4x, 10x/3=300, x=90, so y=400-360=40, the point (90,40).

The other two vertices are at (0,0) and (100,0).

Now we substitute these pairs of values into the revenue expression R=1.95x+2.25y:

(0,0): R=0 (no-brainer!)

(100,0): R=$195

(60,60): R=$117+$135=$252

(90,40): R=$175.50+$90=$265.50–that’s the maximum revenue. 90 standard and 40 deluxe.

You should now be able to fit this solution into the framework of the expected answers to the questions.