let f(x)=x^105+x^53+x^27+x^13+x^3+3x+1.if g(x) is inverse of function f(x),then g'(x) is ?
We have f(x) = y = x^105 + x^53 + x^27 + x^13 + x^3 + 3x + 1
Normally, the inverse function is given by f^(-1)(x) = g(x), where g(x) is gotten by solving the equation y = x^105 + x^53 + x^27 + x^13 + x^3 + 3x + 1 for x, giving x = g(y).
We then write y = g(x) and give the inverse function as f^(-1)(x) = g(x).
However, we cannot solve y = x^105 + x^53 + x^27 + x^13 + x^3 + 3x + 1, for x.
Instead we get the inverse by writing x = y^105+ y^53 + y^27 + y^13 + y^3 + 3y + 1 = h(y).
If we plot the function x = h(y), we will be plotting the inverse function f^(-1)(x) = y.
If we were to plot both f(x) and h(y) (i.e. f^(-1)(x)), we would see that they were reflections of each other about the line y = x.
We would also be able to see what intersection points, if any, there were between the two curves.
The question asks us to find g’(x), the slope of the inverse function, which happens to be:
h(y) = x = y^105+ y^53 + y^27 + y^13 + y^3 + 3y + 1
Differentiating,
dx/dy = 105y^104+ 53y^52 + 27y^26 + 13y^12 + 3y^2 + 3
Therefore,
g’(x) = dy/dx = 1/(dx/dy) = 1/(105y^104+ 53y^52 + 27y^26 + 13y^12 + 3y^2 + 3)
The solution options given for the slope are numerical values, therefore we must be getting asked for the slope at a particular point, which is some value for x and some value for y.
The options for the slope are 3, 1/3 and -1/3.
Looking at the expression for g’(x) = 1/(105y^104+ 53y^52 + 27y^26 + 13y^12 + 3y^2 + 3)
The only viable option is to choose y = 0, giving g’(x) = 1/3
Answer: g’(x) = 1/3
Here is an image of f(x) and h(y) plotted on the same graph.
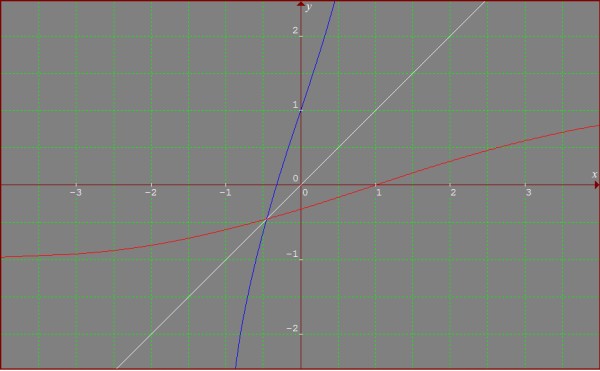
The blue line is: f(x) = y = x^105 + x^53 + x^27 + x^13 + x^3 + 3x + 1
The red line is: h(y) = x = y^105 + y^53 + y^27 + y^13 + y^3 + 3y + 1
The white line is: y = x.
You can see that both curves are reflections of each other about the line y = x.
They have a point of intersection at approx. (-0.5, -0.5)
The intersection of h(y) on the y-axis is at about y = -1/3.
The intersection of h(y) on the x-axis is at x = 1.
These values give an approximate slope, in that area, of 1/3.
This would confirm the value of 1/3 found above for g’(x) at y = 0.