f(x) can be written:
f(x)=1.5+(17x²+7.5x-3.5)/(2x³-x+3).
If u=17x²+7.5x-3.5 and v=2x³-x+3,
then f'(x)=df/dx=(vdu/dx-udv/dx)/v²=
(-34x⁴-30x³+4x²+102x+19)/(2x³-x+3)².
When df/dx=0, -34x⁴-30x³+4x²+102x+19=0.
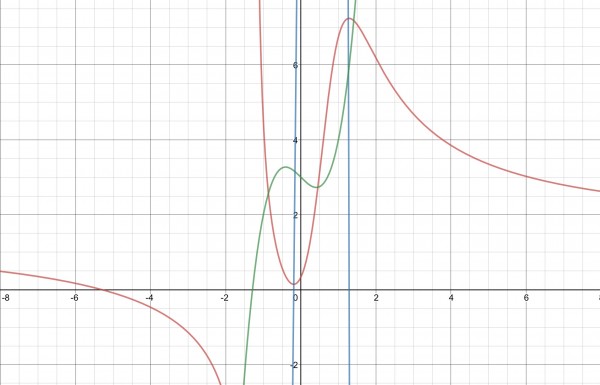
The picture shows f(x) (red), f'(x) (blue) and v (green). There is also an asymptote. The blue curve is only shown as much as it needs to be to indicate where it crosses the x axis.
The turning points can be clearly seen as a minimum and a maximum. f'(x) crosses the x-axis when x is at a turning point. These are the real solutions to f'(x)=0, and Newton’s iterative method can be used to find them. If we start at x₀=-0.2 we can identify the minimum:
x₁=x₀-(-34x₀⁴-30x₀³+4x₀²+102x₀+19)/(-136x₀³-90x₀²+8x₀+102)=-0.1892448 after a couple of iterations, replacing x₀ with x₁ and repeating the calculation to get x₂, and so on, f(x)=0.1426555, so the minimum is (-0.1892,0.1427) approx. With x₀=1.25, we get the maximum turning point for x=1.285976, giving us the point (1.2860,7.2410) approx.