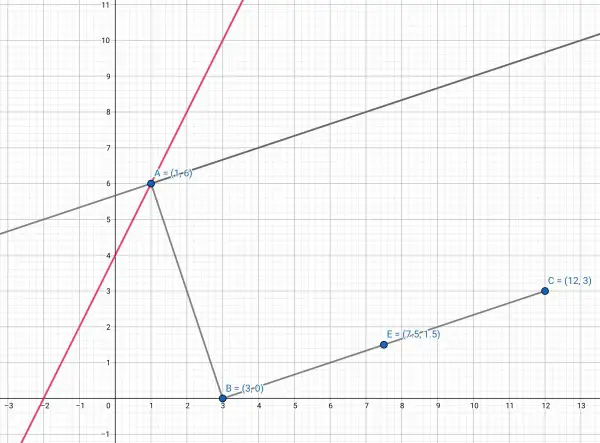
(1) To find the angle of inclination € of BC, we take the slope of BC=3/(12-3)=3/9=⅓. This is the tangent, so the angle is arctan(⅓) or arctan(0.3333)=18.435º.
(2) Slope of AB is -6/(3-1)=-3; slope of BC=⅓.
So AB and BC are perpendicular because -3×1/3=-1. Therefore AD is also perpendicular to AB because AD is parallel to BC.
(3) € is also the angle AD makes with the horizontal, so the line 45º to AD is 45+arctan(⅓). But we want the slope of the line, not the angle, because we need an equation for the line. The slope is the tangent of this angle. We can use the trig identity:
tan(A+B)=(tanA+tanB)/(1-tanAtanB).
A=45, tanB=⅓, so tan(45+arctan(⅓))=(1+⅓)/(1-⅓)=(4/3)/(2/3)=2.
Slope of the line is 2, so we just need a point. (1,6) lies on the line so:
y-6=2(x-1) when we plug in the point.
y=2x-2+6=2x+4, therefore y=2x+4 is the required equation.