Let the slopes of the perspective lines (blue, green and purple in the picture) passing through origin O(0,0) be m₁, m₂, m₃ and let y=m₁x be the line (blue) joining the corresponding generic vertices A of perspective triangles; similarly y=m₂x (green) joins generic vertices B and y=m₃x (purple) joins generic vertices C. (A generic vertex is A, B or C followed by a subscripted index. So, ABC is the generic triangle and AᵣBᵣCᵣ where r=1, 2, etc., identify a particular triangle with the same perspectivity centre O.)
We can define the vertices of three perspective triangles A₁B₁C₁, A₂B₂C₂, A₃B₃C₃:
A₁(a₁,m₁a₁), B₁(b₁,m₂b₁), C₁(c₁,m₃c₁),
A₂(a₂,m₁a₂), B₂(b₂,m₂b₂), C₂(c₂,m₃c₂),
A₃(a₃,m₁a₃), B₃(b₃,m₂b₃), C₃(c₃,m₃c₃).
Triangles A₁B₁C₁ and A₂B₂C₂ determine points on the perspectivity axis, and therefore establish the equation of this axis. The sides A₁B₁ and A₂B₂ (extended as necessary) intersect at some point P; similarly A₁C₁ and A₂C₂ intersect at Q, and B₁C₁ and B₂C₂ intersect at R. The line PQR is the axis. To be in perspective with these triangles, triangle A₃B₃C₃ must be constrained so that A₃B₃ meets A₁B₁ and A₂B₂ at P, A₃C₃ meets A₁C₁ and A₂C₂ at Q, and B₃C₃ meets B₁C₁ and B₂C₂ at R. For the third triangle to be perspective in relation to each of the other two, while the other two remain in perspective (as shown), they must all share the points P, Q and R. There is insufficient space to show this mathematically by deriving the coordinates of these points.
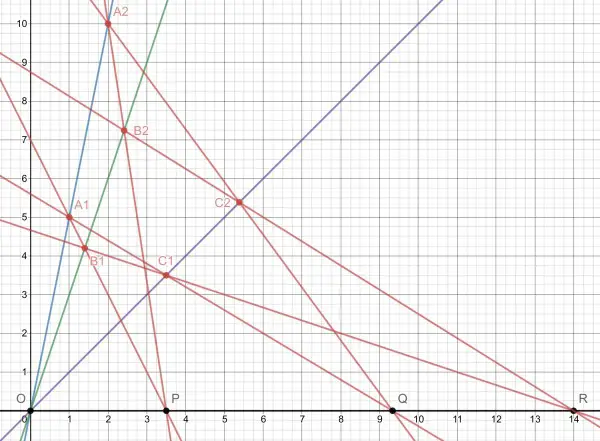
Please note that point O is not necessarily colinear with P, Q and R, but P, Q and R are always colinear. The picture represents a slight simplification for convenience to avoid overcomplication of an already complicated diagram. This does not affect the argument and proof.