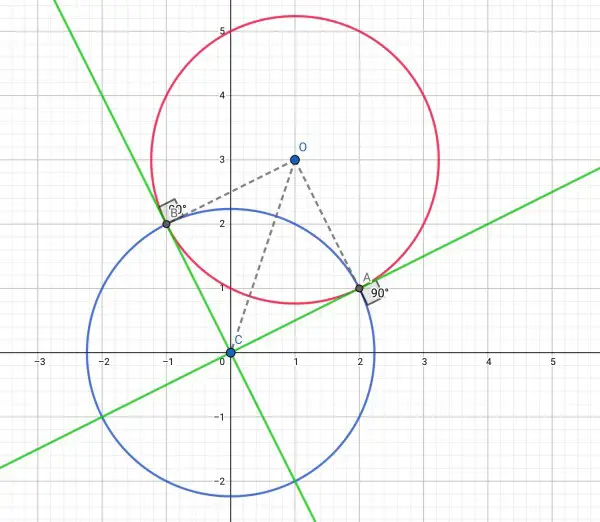
The red circle is the one given.
The equation of the circle can be rewritten by completing the squares.
(x-1)²=x²-2x+1 so x²-2x=(x-1)²-1 and (y-3)²=y²-6y+9, so y²-6y=(y-3)²-9.
Therefore: (x-1)²-1+(y-3)²-9+5=0, (x-1)²+(y-3)²=5, which is a circle radius √5, centre O(1,3) (see picture). The origin is C(0,0)
OC=√(1+9)=√10. OB=OA=√5 (radius). Tangent AC is perpendicular to OA, and tangent BC is perpendicular to OB.
The line L touches the circle at two points A and B. To find them we need to draw another circle (blue). The radius is AC, AC²=OC²-OA²=10-5=5, so the equation of the blue circle is x²+y²=5. This circle intersects the other ((x-1)²+(y-3)²=5) at A and B.
So x²+y²=(x-1)²+(y-3)²=5, x²-(x-1)²+y²-(y-3)²=0, 2x-1+6y-9=0, 2x+6y=10, x+3y=5. Therefore x=5-3y, and we can substitute in x²+y²=5, (5-3y)²+y²=5, 25-30y+10y²=5, 10y²-30y+20=0, y²-3y+2=0=(y-1)(y-2), so the y coords of the points are 1 and 2. So corresponding x values are 5-3=2 and 5-6=-1. The points are A(2,1) and B(-1,2) (see picture). The equation of L are of the form y=mx, so plug in each point to find m: 1=2m, m=½ and 2=-m, m=-2, so L is y=x/2 or y=-2x.