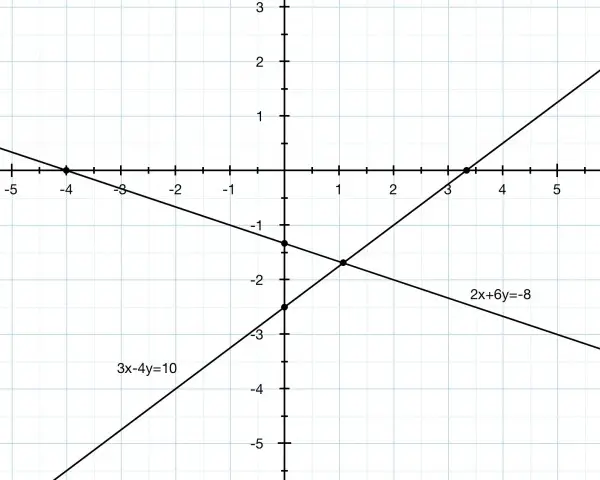
You haven’t listed the points so we have to generalise the answer.
This can be solved graphically. If we plot the equations we can see that the solution is the common area above the intersection point of the two given lines.
We need to work out where the lines intersect. So we remove the inequalities.
From equation 2 we have x=-4-3y, so substitute in equation 1: 3(-4-3y)-4y=10, -12-9y-4y=10, -13y=22, y=-22/13. So x=-4-3y=-4+66/13=14/13, and the intersection point is (14/13, -22/13). The solution to the inequalities is all points above this and enclosed by the two lines. That means that the y coord must be greater than -22/13, otherwise it would lie below the intersection point.
If you had provided a list of points, we would have simply plugged in these points to see which ones satisfied the two inequalities. Or, using the graph, we look to see if the points lie above both lines. For example, (2,1) satisfies the inequalities because it lies in the required area; but (2,-1) doesn’t because it actually lies ON the line, and the inequality needs it to lie ABOVE the line. Also, both (1,1) and (1,-1) satisfy the inequalities, but (-1,-1) doesn’t, and (-1,1) does.