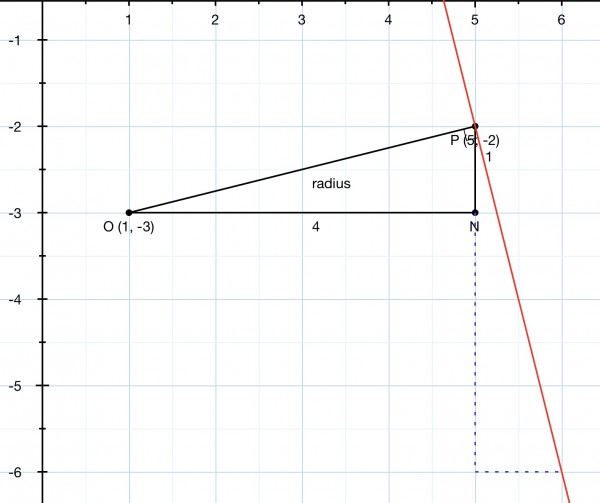
Take a look at the picture above. Note that it’s not necessary to draw the circle to solve this problem, nor is it necessary to know the equation of the circle, or use calculus.
O(1,-3) is the centre of the circle and P(5,-2) the point on the circumference where the tangent is drawn (red line perpendicular to the radius). We can find the slope of the tangent by looking at the geometry. The triangle’s legs are shown in dotted blue (apart from the segment PN) and a segment of the tangent line is shown in red, forming the hypotenuse equal in length to OP. This right triangle is congruent to OPN, so we know its slope is -4 (negative because it slopes backwards).
The slope of the tangent line is the coefficient of the x term in the equation of the line, so it’s -4x. Now we need the y intercept. So we call it a, so that y=-4x+a. We know (5,-2) is on the line so we substitute to find a:
-2=-4×5+a, -2=-20+a, a=18, therefore the line is y=-4x+18 or y=18-4x.
The general form is 4x+y-18=0.