A 1.5 kg block and a 2.5 kg block are attached to opposite ends of a light rope. The rope hangs over a solid, frictionless pulley that is 30 cm in diameter and has a mass of 0.75 kg. When the blocks are released, what is the acceleration of the lighter block?
Assuming that the two blocks are hanging vertically, let the pulley/rope/blocks system be as shown below.
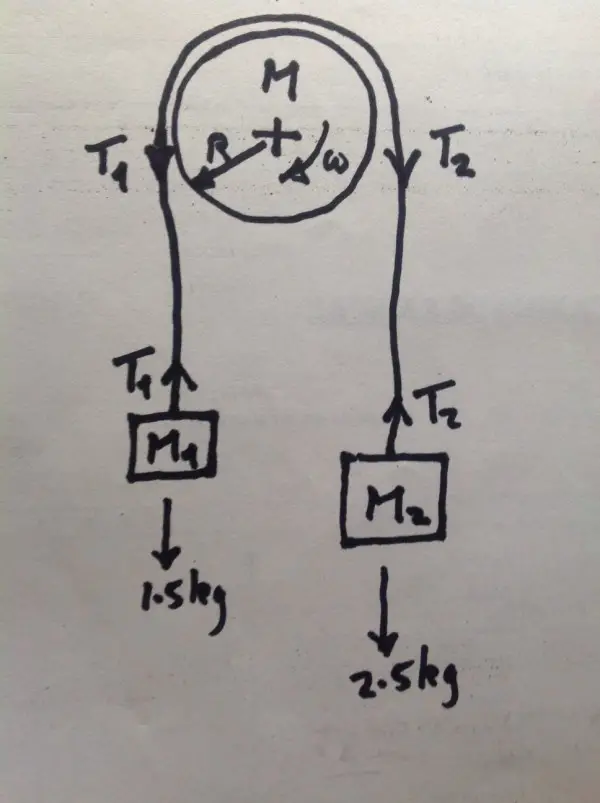
Let F1 be the accelerating force on the 1st block, M1.
Let F2 be the accelerating force on the 2nd block, M2.
By Newton’s 2nd law,
F1 = T1 – 1.5g = M1*a
F2 = 2.5g – T2 = M2*a
Rearranging the above two equations,
T1/1.5 – g = g – T2/2.5
2.5T2 + 1.5T1 = 7.5g
5T1 + 3T2 = 15g
The effective torque applied to the pulley is
τ = (T2 – T1)*R
Using τ = Iα, I = (1/2)MR^2 and a = αR
(T2 – T1)*R = (1/2)MR^2(a/R)
(T2 – T1) = (1/2)aM
Using T1 – 1.5g = M1*a, from above
a = (T1 – 1.5g)/M1 = T1/M1 – g
Substituting for a = T1/M1 – g into (T2 – T1) = (1/2)aM
(T2 – T1) = (1/2)(T1/M1 – g)M
T2 – T1 = 0.5(T1/1.5 – g)*0.75 = 0.25T1 – 0.375g
T2 – 1.25T1 = -0.375g
Substituting for T2 = 1.25T1 – 0.375g, into 5T1 + 3T2 = 15g
5T1 + 3.75T1 – 1.125g = 15g
8.75T1 = 16.125g
T1 = 18.0784 N (k1)
Using 5T1 + 3T2 = 15g,
90.39214 + 3T2 = 15*9.81
T2 = 18.91928 N (k2)
Check
Using a = T1/M1 – g = 18.0784/1.5 – 9.81 = 2.24228 m/s^2 (k3)
Using a = g – T2/M2 = 9.81 – 18.91928/2.5 = 2.24228 m/s^2
The acceleration of both blocks is a = 2.24 m/s^2
For the Pulley
I = (1/2)MR^2 = 0.5*0.75*0.15^2 = 0.0084375 kgm^2
Ang. Accln. Is α = a/R = 2.24228/0.15 = 14.948 ᶜ/s^2
Accelerating torque is τ = Iα = 0.0084375*14.948 = 0.126 13 Nm
τ = (τ1 – τ2) = (T2 – T1)R = (18.91928 – 18.0784) *0.15 = 0.12613 Nm