what is bigger 5/8 or 11/20

Question

my maths question cant quite get the hold of fractions could need some help if willing :L

Answer 1

 

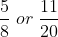
The easiest way to compare these numbers is to put them all over the same denominator. 

If both the top and bottom of a fraction are multiplied or divided by the same divisor, the fraction will stay the same; ie 1/2 - multiplying both top and bottom by 2 gives 2/4 which is the same thing.  

Look for the lowest common multiple of 8 and 20 (or, do a cheat which i do - multiply 8 by 20 to get an answer which is a common multiple)

This answer is 160.

 

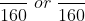
Next, multiply the top of the fraction which had the 8 below it, by 20, and the top of the fraction with 20 below it, by 8.

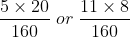
This can now be simplified to 

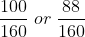
This can now be compared , to see that the 

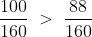
so

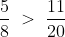
(note, > means the left is bigger than the right. < means the left is smaller than the right.  This can be remembered by 2 ends is more than 1 end, so the bigger number will have the most ends.)

Answer 2

5/8 easy